–Я–Њ–Ї–∞–Ј–∞–љ–Є–µ –Р–Љ–њ–µ—А–Љ–µ—В—А–∞ –њ—А–Є –Т–љ—Г—В—А–µ–љ–љ–µ–Љ –°–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–Є –Ш—Б—В–Њ—З–љ–Є–Ї–∞
пїњ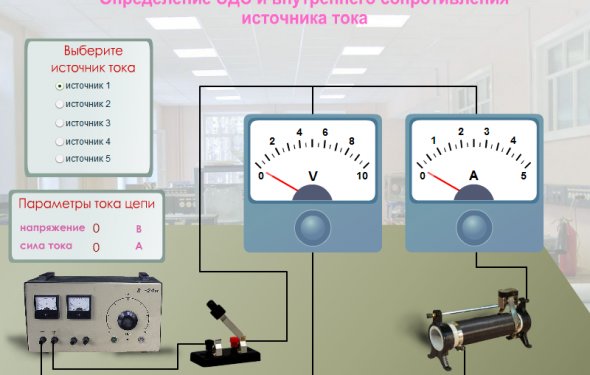
- –≠–ї–µ–Ї—В—А–Є—З–µ—Б–Ї–∞—П —Ж–µ–њ—М —Б–Њ—Б—В–Њ–Є—В –Є–Ј –Є—Б—В–Њ—З–љ–Є–Ї–∞ —В–Њ–Ї–∞ —Б –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –≠–Ф–° –Є –≤–љ—Г—В—А–µ–љ–љ–Є–Љ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–µ–Љ –Є –≤–љ–µ—И–љ–µ–≥–Њ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ—П . –Ю–њ—А–µ–і–µ–ї–Є—В—М, –Ї–∞–Ї –Ј–∞–≤–Є—Б–Є—В –њ–Њ–ї–µ–Ј–љ–∞—П –Љ–Њ—Й–љ–Њ—Б—В—М, –≤—Л–і–µ–ї—П–µ–Љ–∞—П –љ–∞ –≤–љ–µ—И–љ–µ–Љ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–Є, –Є –Ъ–Я–Ф –Є—Б—В–Њ—З–љ–Є–Ї–∞ –≤ —Ж–µ–њ–Є –Њ—В –≤–µ–ї–Є—З–Є–љ—Л –≤–љ–µ—И–љ–µ–≥–Њ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П . –Я–Њ—Б—В—А–Њ–Є—В—М –≥—А–∞—Д–Є–Ї–Є —Н—В–Є—Е –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–µ–є. –Я—А–Є –Ї–∞–Ї–Њ–є –≤–µ–ї–Є—З–Є–љ–µ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ—П —В–µ–њ–ї–Њ–≤–∞—П –Љ–Њ—Й–љ–Њ—Б—В—М, –≤—Л–і–µ–ї—П–µ–Љ–∞—П –≤ –љ–µ–Љ, –±—Г–і–µ—В –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞?
–†–µ—И–µ–љ–Є–µ.
–Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —В–Њ–Ї–∞ —Б–ї–µ–і—Г–µ—В –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –Ј–∞–Ї–Њ–љ–Њ–Љ –Ю–Љ–∞ –і–ї—П –Ј–∞–Љ–Ї–љ—Г—В–Њ–є —Ж–µ–њ–Є
IR+Ir-–Д=0.
–Ю—В—Б—О–і–∞ –њ–Њ–ї—Г—З–∞–µ—В—Б—П —В–Њ–Ї I=–Д/(R+r). –Ь–Њ—Й–љ–Њ—Б—В—М, –≤—Л–і–µ–ї—П—О—Й—Г—О—Б—П –≤ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–Є, —Б–ї–µ–і—Г–µ—В –љ–∞–є—В–Є –њ–Њ –Ј–∞–Ї–Њ–љ—Г –Ф–ґ–Њ—Г–ї—П-–Ы–µ–љ—Ж–∞:
WR=I2R=–Д2R/(R+r)2
–Ь–Њ—Й–љ–Њ—Б—В—М, —А–∞—Б—Е–Њ–і—Г–µ–Љ–∞—П –Є—Б—В–Њ—З–љ–Є–Ї–Њ–Љ —В–Њ–Ї–∞:
W–Д=–ДI=–Д2/(R+r)
–Ґ–Њ–≥–і–∞ –Ъ–Я–Ф —Б–Њ—Б—В–∞–≤–Є—В:
–Ъ–Я–Ф= WR/ W–Д =R/(R+r)
–Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–є –Љ–Њ—Й–љ–Њ—Б—В–Є, –≤—Л–і–µ–ї—П—О—Й–µ–є—Б—П –≤ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–Є, –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ —Г—Б–ї–Њ–≤–Є–µ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ —Д—Г–љ–Ї—Ж–Є–Є:
dWR/dR=–Д2[((R+r)2-2R(R+r)]/ (R+r)4=–Д2(r-R)/(R+r)3=0,
—В.–µ. –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞—П –Љ–Њ—Й–љ–Њ—Б—В—М –≤—Л–і–µ–ї—П–µ—В—Б—П –≤ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–Є –њ—А–Є R=r –Є —Б–Њ—Б—В–∞–≤–ї—П–µ—В
(WR)–Љ–∞–Ї—Б=–Д2/4r
- –Т —Н–ї–µ–Ї—В—А–Є—З–µ—Б–Ї–Њ–є —Ж–µ–њ–Є –Њ–њ—А–µ–і–µ–ї–Є—В—М –њ–Њ–Ї–∞–Ј–∞–љ–Є—П –Є–і–µ–∞–ї—М–љ—Л—Е –≤–Њ–ї—М—В–Љ–µ—В—А–∞ –Є –∞–Љ–њ–µ—А–Љ–µ—В—А–∞. –≠–Ф–° –Є—Б—В–Њ—З–љ–Є–Ї–Њ–≤ —В–Њ–Ї–∞ –Є –Є—Е –≤–љ—Г—В—А–µ–љ–љ–Є–µ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ: –Д1=9 –Т, –Д2= 12–Т, r1=3 –Ю–Љ, r2=4 –Ю–Љ, —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–µ —А–µ–Ј–Є—Б—В–Њ—А–∞ =5 –Ю–Љ. –Ъ–∞–Ї–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —В–µ–њ–ї–∞ –≤—Л–і–µ–ї–Є—В—Б—П –≤ —А–µ–Ј–Є—Б—В–Њ—А–µ –Ј–∞ –≤—А–µ–Љ—П t=10 —Б?
.
–Ш–і–µ–∞–ї—М–љ—Л–є –≤–Њ–ї—М—В–Љ–µ—В—А –Њ–±–ї–∞–і–∞–µ—В –±–µ—Б–Ї–Њ–љ–µ—З–љ—Л–Љ –≤–љ—Г—В—А–µ–љ–љ–Є–Љ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–Љ, –Є–і–µ–∞–ї—М–љ—Л–є –∞–Љ–њ–µ—А–Љ–µ—В—А вАУ –љ—Г–ї–µ–≤—Л–Љ –≤–љ—Г—В—А–µ–љ–љ–Є–Љ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–Љ. –Я–Њ –Ј–∞–Ї–Њ–љ—Г –Ф–ґ–Њ—Г–ї—П-–Ы–µ–љ—Ж–∞ –≤ —А–µ–Ј–Є—Б—В–Њ—А–µ –Ј–∞ –≤—А–µ–Љ—П –≤—Л–і–µ–ї–Є—В—Б—П —Н–љ–µ—А–≥–Є—П Q=I2Rt. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —В—А–µ–±—Г–µ—В—Б—П –љ–∞–є—В–Є —В–Њ–Ї —З–µ—А–µ–Ј —А–µ–Ј–Є—Б—В–Њ—А R.
–Я–Њ –њ–µ—А–≤–Њ–Љ—Г –њ—А–∞–≤–Є–ї—Г –Ъ–Є—А—Е–≥–Њ—Д–∞ –Є–Љ–µ–µ–Љ:
I1+I2=I
–Т—Л–±–µ—А–µ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –Њ–±—Е–Њ–і–∞ –Ї–Њ–љ—В—Г—А–Њ–≤ –њ–Њ —З–∞—Б–Њ–≤–Њ–є —Б—В—А–µ–ї–Ї–µ. –Ф–ї—П –Ї–Њ–љ—В—Г—А–Њ–≤, —Б–Њ–і–µ—А–ґ–∞—Й–Є—Е —А–µ–Ј–Є—Б—В–Њ—А –Є –Є—Б—В–Њ—З–љ–Є–Ї–Є —В–Њ–Ї–∞ –њ–Њ –≤—В–Њ—А–Њ–Љ—Г –њ—А–∞–≤–Є–ї—Г...
- –Р–Љ–њ–µ—А–Љ–µ—В—А –і–ї—П –Ш–Ј–Љ–µ—А–µ–љ–Є—П –Я–µ—А–µ–Љ–µ–љ–љ–Њ–≥–Њ –Ґ–Њ–Ї–∞
- –Т–Њ–ї—М—В–Љ–µ—В—А –Р–Љ–њ–µ—А–Љ–µ—В—А –Я–Њ—Б—В–Њ—П–љ–љ–Њ–≥–Њ –Ґ–Њ–Ї–∞ –°–≤–Њ–Є–Љ–Є –†—Г–Ї–∞–Љ–Є
- –Я–Њ–і–Ї–ї—О—З–µ–љ–Є–µ –Р–Љ–њ–µ—А–Љ–µ—В—А–∞ –І–µ—А–µ–Ј –Ґ—А–∞–љ—Б—Д–Њ—А–Љ–∞—В–Њ—А –Ґ–Њ–Ї–∞
- –Т–Ї–ї—О—З–µ–љ–Є–µ –Р–Љ–њ–µ—А–Љ–µ—В—А–∞ –Є –Т–Њ–ї—М—В–Љ–µ—В—А–∞ –≤ –≠–ї–µ–Ї—В—А–Є—З–µ—Б–Ї—Г—О –¶–µ–њ—М